Extreme rainfall has the potential to generate floods and debris flows, which pose major hazards to populations and infrastructure, resulting in the loss of lives and livelihoods. We have witnessed destructive flooding within the UK during December 2015, leading to substantial economic losses, however the relative losses due to floods and debris flows within developing countries are much larger.
Arguably less well-known, but also of considerable destructive power, are lahars; these are volcanic debris flows, often formed by intense rainfall onto loosely compacted volcanic deposits, and flow as concentrated mixtures of water and solids. Lahars have led to catastrophic events, notably including the 1985 lahar at Navada del Ruiz Volcano, Colombia, which led to over 23,000 fatalities (see Pierson et al. 1990, J. Volcanol. Geotherm. Res. 41, 17-66 and USGS VDAP images).
There is an evident need to improve and refine our capabilities to assess the risk posed by these events and this is what we address in this feasibility project. We combine state-of-the-art modelling of the dynamics of the flowing material with modern statistical techniques for assessing uncertainty to analyse potential floods, debris flows and lahars. This could have a major impact on risk management and consequentially, risk reduction.
In this Maths Foresees project we combine the Shuttle Radar Topography Mission (SRTM) 90m digital elevation database, modern statistical methods for spatial analysis, and recent developments in shallow water modelling. Together these will be used to create a product for assessing flood and lahar risk at the village scale, almost anywhere in the world.
We have assembled a multidisciplinary team to carry out this study:
- Prof. Andrew J. Hogg, School of Mathematics, University of Bristol
- Prof. Jonathan C. Rougier, School of Mathematics, University of Bristol
- Prof. Paul B. Bates, School of Geographical Sciences, University of Bristol
- Dr Mark J. Woodhouse, Schools of Mathematics and Earth Science, University of Bristol
- Prof. Robert Lamb, JBA Trust
Floods, debris flows and lahars are primarily driven by gravitational acceleration. Therefore the accuracy of model prediction is closely tied to the accuracy with which the topography can be represented. In this study we utilise the SRTM database with resolution at 90m, as this digital elevation map (DEM) is freely available and globally connected, allowing incorporation into tools provided to institutions in developing countries; higher resolution data is available in some areas and the methodology we are developing could be more widely applied.
The elevation data is not free from error, and a careful study has been carried out to summarize the error characteristics (Rodriguez et al., 2006, Photogrammetric Engineering & Remote Sensing, 72, 249-260). Modern statistical methods allow us to treat the SRTM digital elevation map (DEM) as an imperfect observation on the underlying true elevation, and in this way to generate a set of spatially coherent candidates for the true elevation, representing the uncertainty in the DEM. This can be a computationally intractable problem with a large spatial field. However, in the last decade there has been very considerable progress in modelling large spatial fields using Gauss Markov Random Fields (e.g. Rue & Held, 2005, Gaussian Markov Random Fields: Theory and Applications), in which the neighbourhood structure of the pixels is encoded as a graph, and sparsity of the precision matrix is used to reduce the computational cost. It turns out that these methods are close to the heuristic methods that hydrologists have been applying in order to generate a single candidate, since they have the appearance of smoothing over a specified neighbourhood, such as, for example, one that is elongated up-slope. However the statistical framework we adopt provides information about the distribution of the uncertainty as well as the 'single candidate' for the topography, which effectively emerges as the expectation.
For any given candidate topography, we model the flow; our approach is to adopt the shallow-water frame-work with two spatial coordinates, fitted to the DEM, and to integrate the governing equations numerically using relatively efficient modern techniques that can be applied over over long channels. The driving downslope gravitational acceleration is then tied to the representation of the topography.
The resistance to the motion is primarily due to basal drag, which if the flowing material is predominantly water can be presented by Chézy drag parameterisation in analogy with hydraulic models. However for debris flows and lahars with high concentrations of solids, the representation of this drag requires a different formulation. For example, an end member is to treat the motion as a lubricated granular flow where a Coulomb basal drag might be a more appropriate model. Importantly, flows are observed to transition between regimes during their propagation.
Particle transport by the flow can be of considerable importance. While for floods, it is likely that the overall concentration of solids remains relatively low and so the presence of suspended solids does not feedback significantly on the dynamics of the motion, it is nevertheless feasible that a flood event leads to substantial sediment transport. For debris flows and lahars, the particle transport is dynamically important and `bulking up' of the flow due to mass entrainment from the bed can alter the resistive force generated by the motion. For example, particle erosion can increase the solids fraction within the flowing material, thus fundamentally changing the nature of interactions between particles, as well as increasing the driving force downslope.
As a preliminary example, we implement our numerical model for a lahar at the Nevada del Ruiz Volcano, Colombia (Figure 1). We use STRM topographic data and an erosion model that expresses the erosive flux in terms the excess Shields parameter of the flow. We note from Figure 1a,b, which depict the flow depth approximately 1 hour after initiation close to the volcano, that when the erosion is included the flows propagate further and faster down slope, thus illustrating the need to include `bulking up' for these flows.
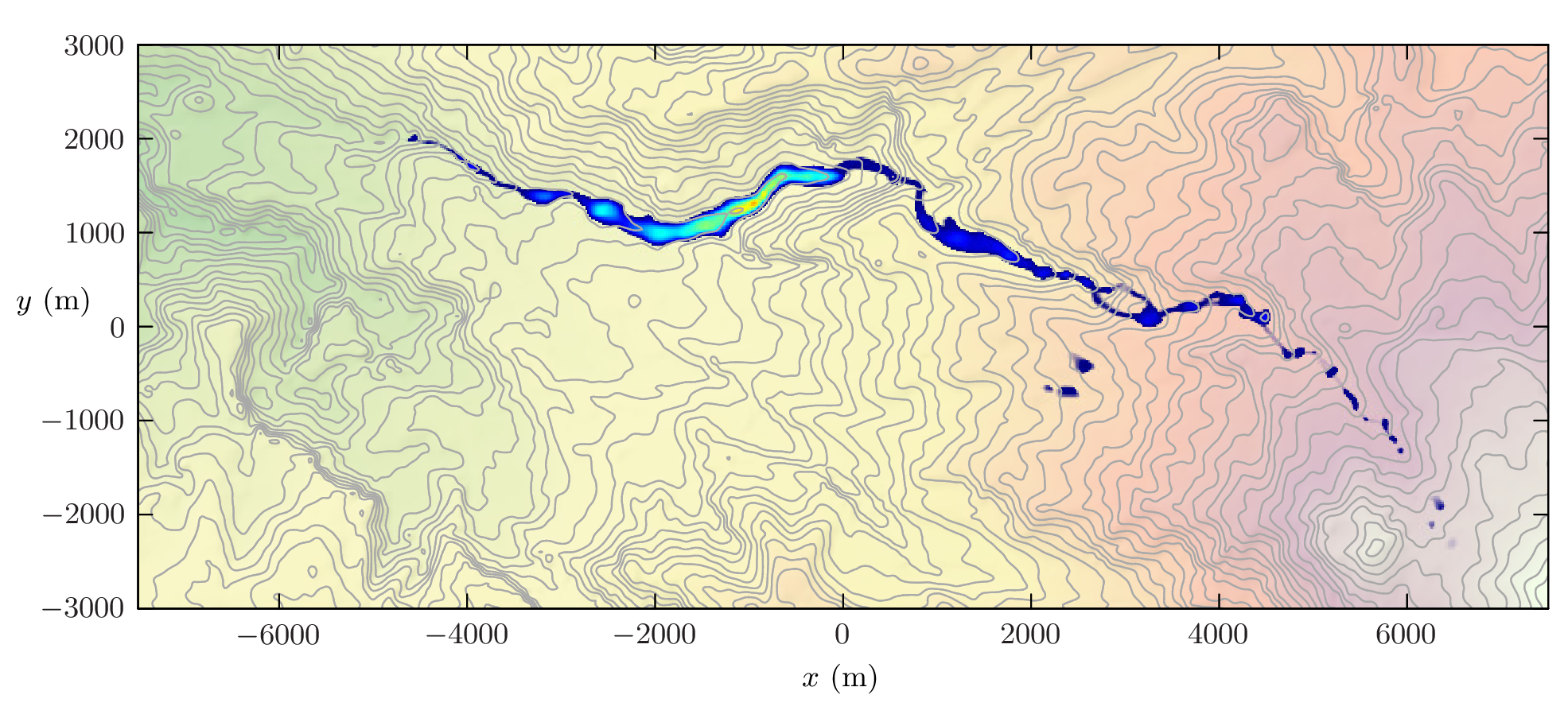
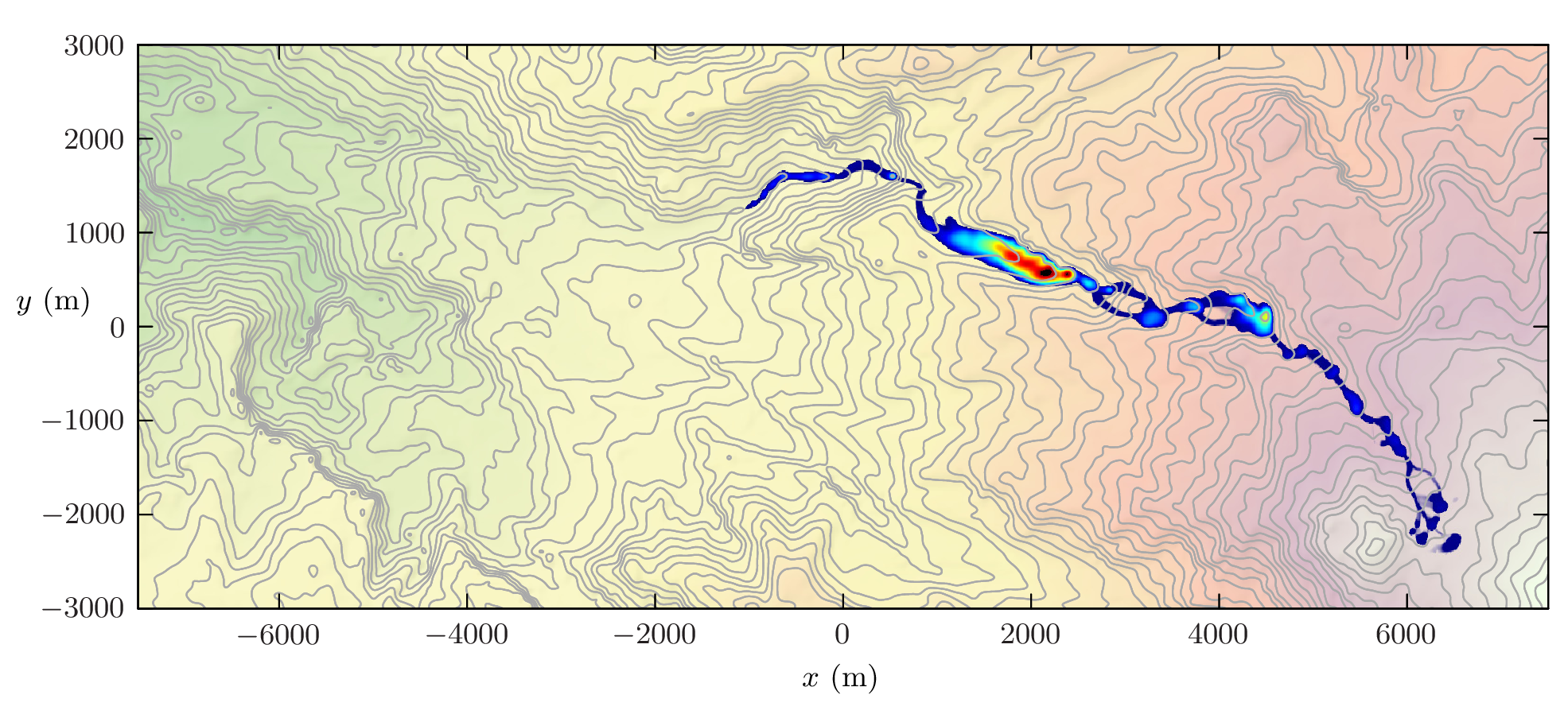
For both dilute sediment transport by floods and mass erosion by debris flows, there is considerable u-certainty in the choice of model for the erosion; in this study we will employ formulations based on erosion driven by the basal shear stress. Importantly, though, since this stress, and consequentially particle entrainment, relies on the downslope driving force exceeding a non-vanishing threshold (such as the critical Shields parameter for erosion, or the frictional Coulomb angle), it is crucial that the slope is accurately determined and that potential errors and uncertainty in its measurements are known as accurately as possible.
The SRTM is the primary source of local elevation information in many remote regions. But the 90m resolution of the SRTM is low on the scale of a channel, and therefore we contend that elevation uncertainty is the dominant source of uncertainty, notwithstanding the challenges of modelling the flow. However, the uncertainty in DEMs is rarely incorporated into hazard assessments even when uncertainty in source conditions is examined. By forcing the flow model with appropriately-selected candidates for the elevation, we can provide a hazard distribution, such as the inundation depth, at a location such as a village, which can in turn be mapped into a loss distribution and a risk assessment. Among other uses, such a tool can be deployed as a tier one assessment for risk, ahead of decisions about where to collect more detailed elevation information.
